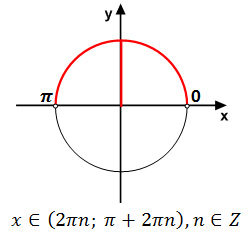
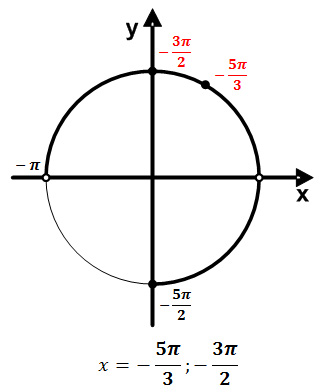
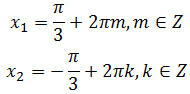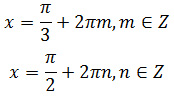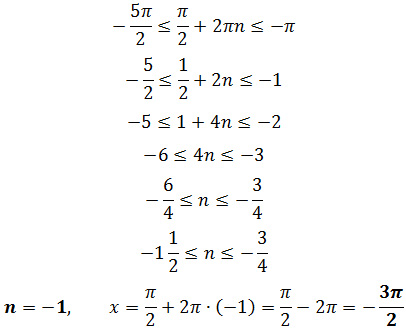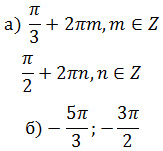Задание 13. ЕГЭ. Решите уравнение (6sin^x + 11cosx — 10)log(sinx)=0

Задание. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку [-5π/2; -π].

Решение:

а) Решите уравнение

ОДЗ уравнения:

sinx > 0

Уравнение состоит из двух множителей. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла, т. е.

Решим 1 уравнение:

6sin²x + 11cosx – 10 = 0

6(1 – cos²x) + 11cosx – 10 = 0

6 – 6cos²x + 11cosx – 10 = 0

– 6cos²x + 11cosx – 4 = 0

6cos²x – 11cosx + 4 = 0

Введем новую переменную, пусть t = cosx

6t² – 11t + 4 = 0

D = (-11)² — 4·6·4 = 25

t₁ = 4/3; t₂ = 1/2

Вернемся к первоначальной переменной, получим

cosx = 4/3   и   cosx = 1/2

Уравнение cosx = 4/3 не имеет решения, т. к. – 1 ≤ cosx ≤ 1

Решим уравнение

cosx = 1/2

Корень x₂ ∉ ОДЗ.

Решим 2 уравнение:

Тогда уравнение

имеет два корня:

б) Найдите все корни этого уравнения, принадлежащие отрезку [-5π/2; -π].

Выберем корни уравнения при помощи единичной окружности с учетом ОДЗ:

Корни уравнения можно выбрать другим способом:

Для первого корня:

Для второго корня:

Ответ:

Понравилось? Нажмите