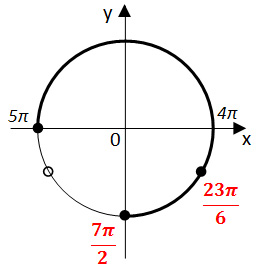
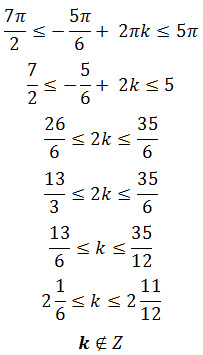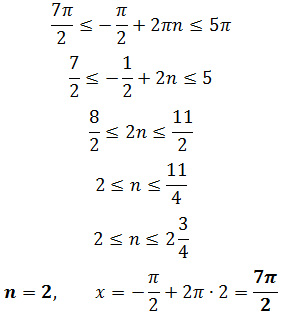Задание 13. ЕГЭ. Решите уравнение 125·625^sinx – 30·25^sinx + 1 = 0.

Задание. а) Решите уравнение 125·625^sinx – 30·25^sinx + 1 = 0.

б) Найдите все корни этого уравнения, принадлежащие отрезку [7π/2; 5π].

Решение:

а) Решите уравнение 125·625^sinx – 30·25^sinx + 1 = 0.

ОДЗ уравнения: R

Преобразуем уравнение, представим 625^sinx = (25²)^sinx = 25^2sinx = (25^sinx)², получим

125·(25^sinx)² – 30·25^sinx + 1 = 0

Введем новую переменную, пусть 25^sinx = а, где а > 0.

Получим уравнение

125а² – 30а + 1 = 0

D = 400

а₁ = 1/5 и а₂ = 1/25

Вернемся к первоначальной переменной, получим 2 уравнения:

25^sinx = 1/5    и     25^sinx = 1/25

Решим 1 уравнение:

25^sinx = 1/5

5^2sinx = 5^-1

2sinx = — 1

sinx = — 1/2

(1)

(2)

Решим 2 уравнение:

25^sinx = 1/25

5^2sinx = 5^-2

2sinx = — 2

sinx = — 1

(3)

б) Найдите все корни этого уравнения, принадлежащие отрезку [7π/2; 5π].

Выберем корни уравнения при помощи единичной окружности

 

Корни уравнения можно выбрать другим способом:

Для первого корня:

Для второго корня:

Для третьего корня:

Ответ:

Понравилось? Нажмите