

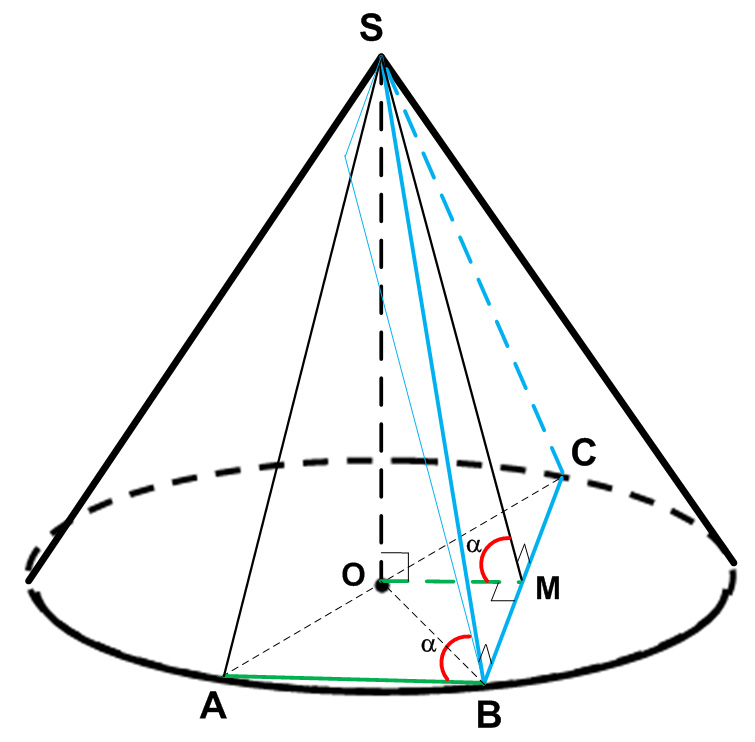
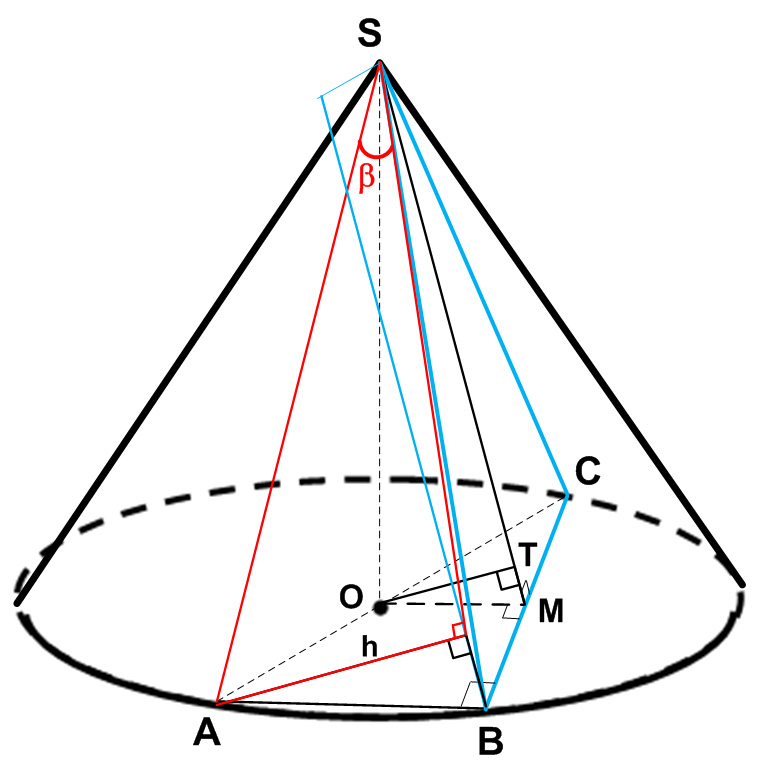
Задание 14. ЕГЭ. Точки А, В и С лежат на окружности основания конуса с вершиной SЗадание. Точки А, В и С лежат на окружности основания конуса с вершиной S, причем А и С диаметрально противоположны. Точка М – середина ВС. а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC. б) Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и SC = 5√2. Решение: а) Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на эту плоскость. Найдем угол между прямой SM и плоскостью АВС. Проекцией точки S на плоскость АВС является точка О – центр основания конуса, точка М лежит в плоскости АВС, следовательно, ОМ – проекция прямой SM на плоскость АВС. Значит, угол между прямой SM и плоскостью АВС – это угол ∠SMO (на рисунке ∠α). SО ⊥ (АВС), ОМ ⊥ ВС (т. к. ΔВОС – равнобедренный и точка М – середина ВС), тогда SM ⊥ ВС (по теореме о трех перпендикулярах). Прямая АВ ⊥ ВС (т. к. ∠АВС = 900, вписанный в окружность угол и опирающийся на диаметр АС). Прямая АВ параллельна ОМ, следовательно, угол между прямой АВ и плоскостью SBC такой же, как и угол между прямой SM и плоскостью АВС. б) Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и SC = 5√2. Найдем угол между прямой SA и плоскостью SBC. Опустим перпендикуляр h на плоскость SBC, тогда ∠β — искомый угол. Перпендикуляр h на плоскость SBC – это расстояние от точки А до плоскости SBC. ОТ – расстояние от точки О до плоскости SBC. Так как точка О – середина АС, то h = 2·OT ОТ – высота прямоугольного треугольника ΔOSM, проведенная из вершины прямого угла. Так как ΔOTM подобен ΔSOM, то Так как ОМ – средняя линия треугольника ΔАВС: OM = 3 Из прямоугольного треугольника ΔSMC: SM2 = SC2 – MC2 МС = 1/2 · ВС = 4 Из прямоугольного треугольника ΔOSM: SO2 = SM2 – OM2 Подставим полученные данные в формулу (1): SA = SC = 5√2 Найдем sinβ: Ответ: Оставить комментарий |
Рубрики
|
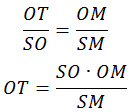 (1)
(1)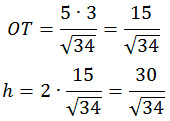

В очередной раз большое спасибо. Четко и понятно. Главное, уделяете внимание «узким местам»
в решении.
Спасибо Вам за пояснения!