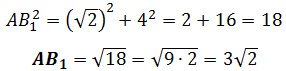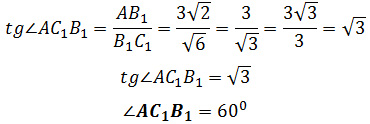Задание 14. ЕГЭ. В цилиндре образующая перпендикулярна плоскости основания.

Задание. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С₁, причем СС₁ – образующая цилиндра, а АС – диаметр основания. Известно, что ∠АСВ = 30⁰, АВ = √2, СС₁ = 4.

а) Докажите, что угол между прямыми АС₁ и ВС равен 60⁰.

б) Найдите площадь боковой поверхности цилиндра.

Решение:

а) Докажите, что угол между прямыми AС₁ и BС равен 60⁰.

Проведем образующую ВВ₁, тогда ВВ₁С₁С – прямоугольник и ВС параллельна В₁С₁, поэтому угол между прямыми АС₁ и ВС равен углу между прямыми АС₁ и В₁С₁, т. е. равен углу ∠АС₁В₁.

Угол ∠АВС – вписанный в окружность угол, который опирается на диаметр основания цилиндра, следовательно, ∠АВС = 90⁰ и треугольник ΔАВС – прямоугольный треугольник.

Так как ВС ⊥ АВ и ВС ⊥ ВВ₁, тогда ВС ⊥ (АВВ₁).

Прямая ВС параллельна В₁С₁, значит В₁С₁ ⊥ (АВВ₁) и В₁С₁ ⊥ АВ₁, т. е. треугольник ΔАВ₁С₁ – прямоугольный треугольник (∠АВ₁С₁ = 90⁰).

Тогда

(1)

Так как угол ∠АСВ = 30⁰, а треугольник ΔАВС – прямоугольный треугольник, найдем ВС:

B₁C₁ = BC = √6

Так как ВВ₁ ⊥ (АВС), то треугольник ΔАВВ₁ – прямоугольный треугольник,

по теореме Пифагора найдем В₁С₁:

АВ₁² = АВ² + ВВ₁²

Подставим значения AВ₁ и В₁С₁ в формулу (1), получим

б) Найдите площадь боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту:

Высота цилиндра h равна образующей цилиндра CC₁:

h = CC₁ = 4.

Радиус окружности равен половине диаметра АС:

Из прямоугольного треугольника ΔАВС, найдем AС:

Тогда

Ответ: 8√2π

Понравилось? Нажмите