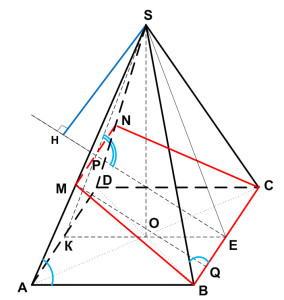
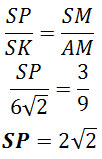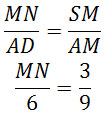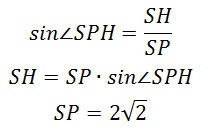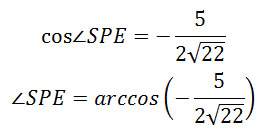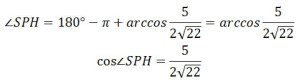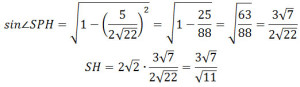Задание 14. Математика ЕГЭ. В правильной четырехугольной пирамиде SABCD найдите расстояние от вершины S до плоскости ВСМ.

Задание.

В правильной четырехугольной пирамиде SABCD основание ABCD – квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что АМ = 6.

а) Постройте перпендикуляр из точки S на плоскость ВСМ.

б) Найдите расстояние от вершины S до плоскости ВСМ.

Решение:

а) Постройте перпендикуляр из точки S на плоскость ВСМ.

Построим плоскость BCM. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Плоскость BCM пересекает основание пирамиды по прямой BC. Так как точки B и M лежат в одной плоскости SAB, то плоскость BCM пересекает грань SAB по прямой BM. Плоскость BCM пересекает грань SAD по прямой MN, проходящей через точку М, параллельно AD (если бы прямая MN была не параллельна AD, то прямая MN должна пересекать прямую AD, принадлежащую основанию в точке, лежащей на прямой ВС, так как все точки плоскости BCM и основания пирамиды лежат на прямой ВС, а это невозможно, так как ВС параллельна AD). Так как точки N и С лежат в одной плоскости SDC, то плоскость BCM пересекает грань SDC по прямой NC. Сечение пирамиды плоскостью BCM представляет собой равнобедренную трапецию BMNC с основаниями BC и MN.

Построим перпендикуляр из точки S на плоскость BCM. Проведем КЕ параллельно АВ, точка Е – середина ВС, точка К – середина AD. Плоскость SKE перпендикулярна плоскости основания, так как проходит через высоту правильной пирамиды. Плоскость SKE пересекает плоскость BCM по прямой РЕ. Тогда перпендикуляром из точки S на плоскость BCM будет являться высота треугольника ∆SPE, проведенная к стороне PE. Выясним, где будет лежать высота треугольника ∆SPE, внутри треугольника или вне его. Для этого определим величину угла ∠SPE.

Рассмотрим треугольник ∆SPE, по теореме косинусов найдем косинус угла ∠SPE.

SE² = PS² + PE² — 2·PS·PE·cos∠SPE

(1)

Из прямоугольного треугольника ∆SСЕ:

SE² = SC² – CE²

SE² = 9² – 3² = 72

SE = 6√2

SE = SK = 6√2

Треугольники ∆MPS и ∆AKE подобны, тогда

Треугольники ∆SMN и ∆SAD подобны, тогда

MN = 2

Рассмотрим равнобедренную трапецию BMNC с основаниями BC и MN, проведем MQ параллельно PE, MQ = PE. Найдем MQ.

Из прямоугольного треугольника ∆SBЕ:

Из треугольника ∆AMB по теореме косинусов найдем МВ:

MB² = AM² + AB² — 2·AM·AB·cos∠MAB

Так как пирамида правильная, то ∠MAB = ∠SBE и cos∠MAB = cos∠SBE.

MB² = 6² + 6² — 2·6·6·(1/3)

MB² = 48

MB = 4√3

Из прямоугольного треугольника ∆MBQ:

MQ² = MB² – BQ²

MQ² = (4√3)² – 2² = 44

MQ = √44

PE = MQ = √44

В формулу (1) подставим полученные значения:

Так cos∠SPE < 0, то угол ∠SPE – тупой, следовательно, высота треугольника∆SPE, проведенная к стороне PE, лежит вне этого треугольника на продолжении стороны PE. Высотой треугольника∆SPE является перпендикуляр SH, проведенный из точки S на плоскость BCM. Искомый перпендикуляр построен (см. рисунок).

б) Найдите расстояние от вершины S до плоскости ВСМ.

Расстоянием от точки до плоскости является перпендикуляр, проведенный из точки на данную плоскость. В нашем случае расстоянием от вершины S до плоскости BCM перпендикуляр SH.

Рассмотрим прямоугольный  треугольника ∆SHP:

Найдем sin∠SPH:

Углы ∠SPH и ∠SPЕ – смежные углы, тогда ∠SPH = 180° – ∠SPЕ

Используя формулу

Получим:

Тогда

Используя основную тригонометрическую формулу sin²α + cos²α = 1, получим sin²α = 1 – cos²α, т.е.

Итак, расстояние от вершины S до плоскости BCM — это длина перпендикуляра SH.

Ответ:

Понравилось? Нажмите