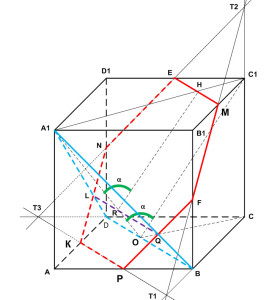
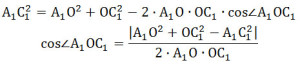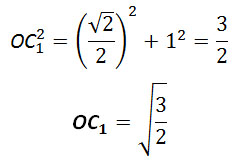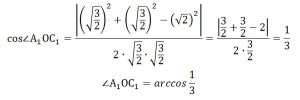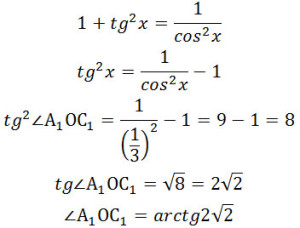Задание 14. Математика ЕГЭ. Дан куб ABCDA1B1C1D1. Найдите угол между плоскостью A1BD и плоскостью, проходящей через середины ребер AB, B1C1, AD.Задание. Дан куб ABCDA1B1C1D1. а) Постройте сечение куба плоскостью, проходящей через середины его ребер AB, B1C1, AD. б) Найдите угол между плоскостью A1BD и плоскостью, проходящей через середины ребер AB, B1C1, AD. Решение: а) Постройте сечение куба плоскостью, проходящей через середины его ребер AB, B1C1, AD. Пусть точки P, M и K – середины ребер AB, B1C1, AD соответственно. Построим плоскость MPK. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Точки Р и К секущей плоскости принадлежат ребрам куба, поэтому Р и К – вершины многоугольника-сечения, а отрезок РК – его сторона. Построим остальные вершины и стороны сечения. Прямая РК расположена в одной плоскости АВС с прямыми ВС и DС, пересекает эти прямые соответственно в точках Т1 и Т3. Поэтому Т1 лежит в плоскости АВС (как точка прямой ВС) и Т1 лежит в плоскости сечения (как точка прямой РК), значит, Т1 – точка пересечения секущей плоскости и прямой ВС. Аналогично, Т3 лежит в плоскости АВС (как точка прямой DC) и Т3 лежит в плоскости сечения (как точка прямой РК), значит, Т3 – точка пересечения секущей плоскости и прямой DC. В плоскости ВСС1 лежат точки Т1 и М, принадлежащие секущей плоскости, поэтому Т1М – прямая пересечения секущей плоскости и плоскости ВСС1. Прямая Т1М расположена в одной плоскости ВСС1 с прямыми ВВ1 и СС1, пересекает эти прямые соответственно в точках F и Т2. Поэтому F лежит в плоскости ВСС1 (как точка прямой ВВ1) и F лежит в плоскости сечения (как точка прямой Т1М), значит, F – точка пересечения секущей плоскости и прямой ВВ1; точка F – еще одна вершина многоугольника-сечения, а отрезки FM и PF – его стороны. Аналогично, точка Т2 – точка пересечения прямой Т1М и СС1 есть точка пересечения секущей плоскости с прямой СС1. Прямая Т2Т3 – прямая пересечения секущей плоскости и плоскости DCC1 пересекает ребра D1C1 и DD1 соответственно в точках E и N, которые также являются вершинами многоугольника-сечения данного куба. Тогда отрезки ME, NE и NK – стороны этого сечения. Таким образом, получаем многоугольник KPFMEN – искомое сечение данного куба плоскостью MPK. Отрезки PK, NE и NK проводим штриховыми линиями, как невидимые. б) Найдите угол между плоскостью A1BD и плоскостью, проходящей через середины ребер AB, B1C1, AD. Построим плоскость A1BD, для этого соединим точки A1, B и D. Треугольник ∆ A1BD – секущая плоскость A1BD. Плоскость A1BD и плоскость МРК имеют общие точки пересечения L и Q, значит, эти плоскости пересекаются по прямой LQ. Найдем угол между плоскостями A1BD и МРК. КР – средняя линия треугольника ABD, значит, KP параллельна BD, а BD лежит в плоскости A1BD, значит, KP параллельна плоскости A1BD. Получим, LQ параллельна KP и LQ параллельна BD. Треугольник ∆ A1BD – равнобедренный, тогда А1О – медиана и высота, А1О перпендикулярна BD и LQ. Аналогично, С1О перпендикулярна BD и LQ, значит, С1О параллельна RH. Следовательно, угол ∠А1RH – линейный угол между плоскостями A1BD и МРК. Угол ∠А1RH равен углу ∠А1ОС1. Рассмотрим треугольник ∆ А1ОС1. Так как за величину угла между двумя плоскостями берется величина острого двугранного угла (взят модуль), по теореме косинусов найдем величину угла ∠А1ОС1, получим Пусть ребро куба равно 1. Рассмотрим треугольник ∆АВС: АС2 = АВ2 + ВС2 АС2 = 12 + 12 = 2 АС = √2 А1С1 = АС = √2 ОС = √2/2 Рассмотрим треугольник ∆ОСС1: ОС12 = ОС2 + СС12 ОА1 = ОС1. Подставим полученные значения в формулу (1): P.S. Так как угол ∠А1ОС1 – угол первой четверти, то tg∠А1ОС1 > 0. Воспользуемся формулой: Ответ: Оставить комментарий |
Рубрики
|