

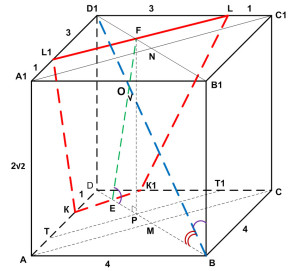
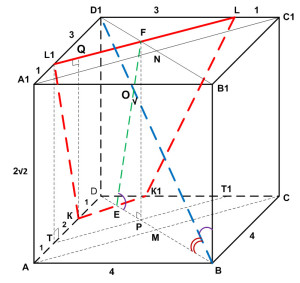
Задание 14. Математика ЕГЭ. Дана правильная четырехугольная призма ABCDA1B1C1D1. Найдите объем пирамиды, вершина которой является точка A1, а основанием – сечение данной призмы плоскостью γ.Задание. Дана правильная четырехугольная призма ABCDA1B1C1D1, сторона AB основания которой равна 4, а боковое ребро AA1 равно 2√2. На ребрах AD и C1D1 отмечены точки K и L соответственно, причем DK = C1L = 1. Плоскость γ проходит через точки K и L и параллельна прямой AC. а) Докажите, что плоскость γ перпендикулярна прямой BD1. б) Найдите объем пирамиды, вершина которой является точка A1, а основанием – сечение данной призмы плоскостью γ. Решение: а) Докажите, что плоскость γ перпендикулярна прямой BD1.
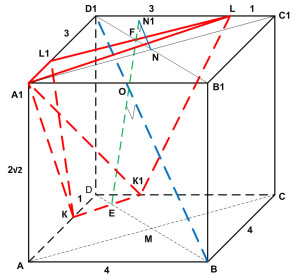
Через точки K и L проведем прямые параллельные АС. Эти прямые пересекают ребра A1D1 и DC в точках L1 и K1 соответственно. Тогда трапеция KL1LK1 является сечением исходной призмы плоскостью γ. Рассмотрим плоскость BDD1. Плоскость BDD1 пересекает прямые КК1 и LL1 в точках E и F соответственно. Следовательно, плоскость сечения KL1L и плоскость BDD1 пересекаются по прямой FE. Четырехугольник BDD1В1 – прямоугольник. Прямая BD1 лежит в плоскости BDD1, значит, прямая BD1 пересекает прямую FE и плоскость KL1L в точке О. Докажем, что плоскость KL1L перпендикулярна прямой BD1. Рассмотрим треугольник ∆ВЕО. Если угол ∠ЕОВ = 90°, то, по свойству прямоугольного треугольника, сумма острых углов треугольника ∆ВЕО должна равняться 90°, т. е. ∠ОЕВ + ∠ЕВО = 90°. Найдем эти углы. Проведем перпендикуляр FP. Из прямоугольного треугольника ∆EFP найдем тангенс угла ∠OEP: FP = AA1 = 2√2 Из прямоугольного треугольника ∆АВС по теореме Пифагора найдем АС: АС2 = АВ2 + ВС2 АС2 = 42 + 42 = 32 АС = 4√2 АС = BD = 4√2 DM = 1/2·BD DM = 2√2 Треугольники ∆DKK1 и ∆DAC подобные треугольники, тогда Через точку Р проведем ТТ1 параллельно КК1, треугольники ∆DTT1 и ∆DKK1 подобные треугольники, тогда EP = DP – DE Получим: Угол ∠ЕВО = 90° – ∠D1BB1. Из прямоугольного треугольника ∆BB1D1 найдем тангенс угла ∠D1BB1: B1D1 = BD = 4√2 BB1 = AA1 = 2√2 Получим: Тогда сумма углов: ∠ЕОВ = ∠ОЕВ + ∠ЕВО = ∠ОЕВ + 90° – ∠ ОЕВ = 90° Следовательно, прямая BD1 перпендикулярна прямой FE. Прямая КК1 параллельна прямой АС, которая перпендикулярна плоскости BDD1. Значит, прямые КК1 и FE перпендикулярны прямой BD1, поэтому прямая BD1 перпендикулярна плоскости сечения γ. б) Найдите объем пирамиды, вершина которой является точка A1, а основанием – сечение данной призмы плоскостью γ. Объем пирамиды A1KL1LK1 (см. рисунок) равен: Высотой пирамиды A1KL1LK1 (см. рисунок) будет являться расстояние от точки А1 до плоскости γ. Точка N – точка пересечения A1C1 и B1D1. Так как прямая A1C1 параллельна плоскости γ, то расстояние от точки А1 до плоскости γ равно расстоянию от точки N до прямой FE. Опустим перпендикуляр из точки N на прямую FE. Так как прямая NN1 перпендикулярна FE, то NN1 перпендикулярна плоскости γ, т. е. NN1 – высота пирамиды A1KL1LK1. FN = D1N – D1F D1N = DM = 2√2 D1F = DP = (3√2)/2 Так как BD параллельна B1D1, а BD1 параллельнаNN1, то угол ∠DBD1 = ∠FNN1. Из прямоугольного треугольника ∆DBD1: BD12 = BD2 + DD12 BD12 = (4√2)2 + (2√2)2 = 32 + 8 = 40 BD1 = 2√10 Из прямоугольного треугольника ∆FNN1: Основанием пирамиды A1KL1LK1 является равнобедренная трапеция KL1LK1, площадь которой равна: Из прямоугольного треугольника ∆DKK1 по теореме Пифагора найдем КК1: КК12 = DK2 + DK12 КК12 = 12 + 12 =2 KK1 = √2 Из прямоугольного треугольника ∆D1L1L по теореме Пифагора найдем LL1: LL12 = D1L12 + D1L2 LL12 = 32 + 32 = 18 LL1 = 3√2 Из прямоугольного треугольника ∆TL1K по теореме Пифагора найдем KL1: KL12 = KT2 + TL12 KL12 = 22 + (2√2)2 = 12 KL1 = 2√3 Из прямоугольного треугольника ∆KQL1 по теореме Пифагора найдем KQ: KQ2 = KL12 – L1Q2 L1Q = (LL1 – КК1)/2 = (3√2 – √2)/2 = √2 KQ2 = (2√3)2 – (√2)2 = 10 KQ = √10 Подставим полученные данные в формулу объема: Оставить комментарий |
Рубрики
|
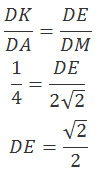
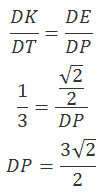

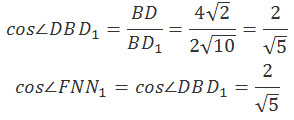
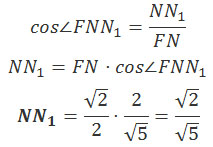
Как связаться с вами, почему нельзя было пункт
а) решить таким образом. Если мы строили плоскость параллельно AC , то можно было доказать , что BD1 перпендикулярно всей плоскости , то она перпендикулярна и прямой лежащей в ней, а если доказали , что она перпендикулярна прямой AC , то она перпендикулярна любой прямой параллельной ей, то есть она перпендикулярна полости y.
По признаку перпендикулярности прямой и плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости. Поэтому доказательства перпендикулярности BD1 к прямой АС недостаточно.