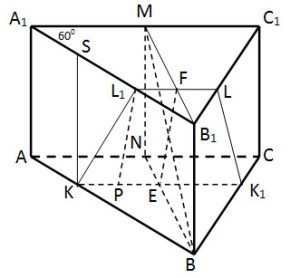
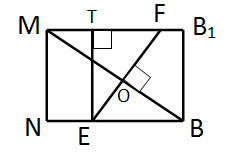
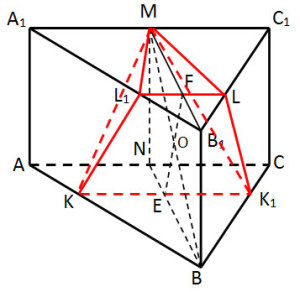
Задание 14. Математика ЕГЭ. Дана правильная треугольная призма ABCA1B1C1, сторона AB основания которой равна 32, а боковое ребро BB1 равно 4√3.

Задание. 

Дана правильная треугольная призма ABCA₁B₁C₁, сторона AB основания которой равна 32, а боковое ребро BB₁ равно 4√3. На ребрах AB и B₁C₁ отмечены  точки K и L соответственно, причем AK = 2; B₁L = 28. Точка M – середина ребра A₁C₁. Плоскость γ проходит через точки K и L и параллельна прямой AC.

а) Докажите, что плоскость γ перпендикулярна прямой BM.

б) Найдите объем пирамиды, вершиной которой является точка M, а основанием – сечение данной призмы плоскостью γ.

рис.1.

Решение:

a) Докажите, что плоскость γ перпендикулярна прямой BM.

Проведем через точки K и L прямые, параллельные AC. Эти прямые пересекают ребро BC в точке K₁ и ребро A₁B₁ в точке L₁ (см. рис. 1). Тогда равнобедренная трапеция KL₁LK₁ является сечением призмы ABCA₁B₁C₁ плоскостью γ.

Рассмотрим плоскость BB₁M. Эта плоскость пересекает прямую AC в точке N, прямую KK₁ в точке E и прямую LL₁ в точке F. Четырехугольник BB₁MN – прямоугольник.

Рассмотрим прямоугольный треугольник A₁MB₁.

MB₁ = A₁B₁·sin60⁰

MB₁ = NB = 16√3.

Рассмотрим прямоугольный треугольник MB₁B. По теореме Пифагора найдем MB.

MB² = MB₁² + BB₁²

MB² = (16√3)² + (4√3)² = 816 = 16·51

MB = 4√51.

По теореме Фалеса:

NE : NB = AK : AB = 2 : 32 = 1 : 16

NE : NB =1 : 16

NE = NB/16

NE = (16√3)/16 = √3.

По теореме Фалеса:

B₁F : MB₁ = B₁L : B₁C₁ = 28 : 32 = 7 : 8.

B₁F : MB₁ = 7 : 8.

B₁F = 7·MB₁/8

B₁F = (7·16√3)/8 = 14√3.

Проведем KS параллельно AA₁. Рассмотрим прямоугольный треугольник KSL₁:

KS = AA₁ = 4√3

SL₁ = A₁L₁ — A₁S

A₁L₁ = A₁B₁ — B₁L = 32 – 28 = 4

A₁S = AK = 2

SL₁ = 2

По теореме Пифагора:

KL₁² = KS² + SL₁²

KL₁² = (4√3)² + 2² = 52

KL₁ = √52

Треугольник ABC и треугольник KBK₁ подобные треугольники, значит

AC : KK₁ = AB : KB

32 : KK₁ = 32 : 30

KK₁ = 30.

Треугольник A₁B₁C₁ и треугольник L₁B₁L подобные треугольники, значит

A₁C₁ : LL₁ = A₁B₁ : B₁L₁

32 : LL₁ = 32 : 28

LL₁ = 28.

Рассмотрим равнобедренную трапецию KL₁LK₁, EF – высота трапеции.

Проведем PL₁ параллельно EF, тогда KP = (KK₁ — LL₁)/2 = 1.

Рассмотрим прямоугольный треугольник KPL₁. По теореме Пифагора:

PL₁² = KL₁² – KP²

PL₁² = (√52)² —  1²  = 52 – 1 = 51

EF = PL₁ = √51.

Рассмотрим рисунок 2.

рис. 2.

Из прямоугольного треугольника MBB₁:

Из прямоугольного треугольника TEF:

Рассмотрим треугольник MFO:

То есть прямые MB и EF перпендикулярны. Прямая KK₁ параллельна прямой АС, которая перпендикулярна плоскости BB₁M. Значит, прямые KK₁ и EF перпендикулярны прямой MB, поэтому прямая MB перпендикулярна плоскости γ.

б) Найдите объем пирамиды, вершиной которой является точка M, а основание – сечение данной призмы плоскостью γ. Смотри рисунок 3.

рис. 3.

Объем пирамиды равен:

Так как MB перпендикулярна плоскости сечения  γ, то MO — высота пирамиды.

Рассмотрим треугольник MEF (рис. 2). Найдем площадь этого треугольника:

TE = BB_1,

MF =MB₁  — B₁F = 16√3 — 14√3 = 2√3

Площадь треугольник MEF можно найти другим способом:

MO = 2S/EF

Площадь основания пирамиды — это площадь сечения, т.е. площадь трапеции KL₁LK_1.

Ответ: 232

Понравилось? Нажмите