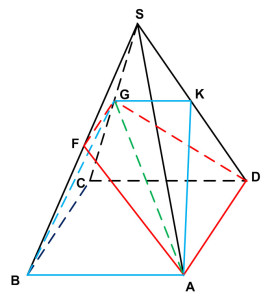
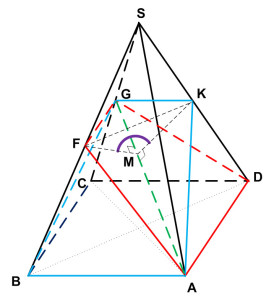
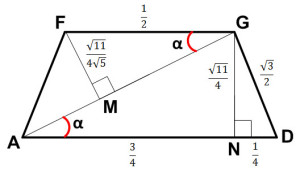
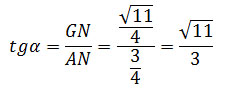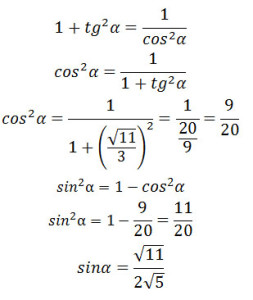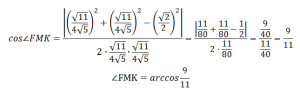Задание 14. Математика ЕГЭ. В правильной четырехугольной пирамиде SABCD все ребра равны 1. Точка F – середина ребра SB, G – середина ребра SC.

Задание.

В правильной четырехугольной пирамиде SABCD все ребра равны 1. Точка F – середина ребра SB, G – середина ребра SC.

а) Постройте прямую пересечения плоскостей ABG и GDF.

б) Найдите угол между плоскостями ABG и GDF.

Решение:

а) Постройте прямую пересечения плоскостей ABG и GDF.

Построим плоскость ABG. Прямая АВ параллельна CD, CD лежит в плоскости SCD, следовательно, АВ параллельна плоскости SCD. Точка G лежит в плоскостях ABG и SCD. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В данном случае плоскость ABG пересекает плоскость SCD по прямой GK, параллельной АВ. Точки А и К лежат в одной плоскости, проведем прямую АК. Сечение плоскостью ABG построено.

Аналогично построим плоскость GDF. Прямая AD параллельна ВС, ВС лежит в плоскости SBC, следовательно, AD параллельна плоскости SBC. Точка G лежит в плоскостях GDF и SВС. Плоскость GDF пересекает плоскость SBC по прямой GF, параллельной AD. Точки А и F лежат в одной плоскости, проведем прямую АF. Сечение плоскостью GDF построено.

Точка  G лежит в плоскостях ABG и GDF. Точка А также лежит в плоскостях ABG и GDF. Следовательно, плоскости ABG и GDF пересекаются по прямой AG. Прямая AG – искомая прямая пересечения плоскостей ABG и GDF.

б) Найдите угол между плоскостями ABG и GDF.

Найдем угол между плоскостями ABG и GDF. Построим линейный угол двугранного угла FAGK. Треугольники ∆AFG и ∆AKG равны по трем сторонам. Тогда перпендикуляры, проведенные из точек F и K к ребру AG двугранного угла  FAGK, попадут в общую точку М. Следовательно, угол ∠FMK – угол между плоскостями ABG и GDF.

Найдем величину этого угла. Рассмотрим треугольник ∆FMK. Так как за величину угла между двумя плоскостями берется величина острого двугранного угла (взят модуль), по теореме косинусов найдем величину угла ∠FMK.

FK² = FM² + MK² – 2·FM·MK·cos∠FMK

Из прямоугольного треугольника ∆ABD по теореме Пифагора найдем BD:

BD² = AB² + AD²

BD² = 1² + 1² = 2

BD = √2

Так как точки F и К – середины ребер SB и SD треугольника ∆SBD, то FK – средняя линия ∆SBD.

FK = 1/2·BD

FK= √2/2

Из прямоугольного треугольника ∆ABF по теореме Пифагора найдем AF:

AF² = AB² – BF²

AF² = 1² – (1/2)² = 3/4

AF = √3/2

GD = √3/2

Так как точки F и G – середины ребер SB и SC треугольника ∆SBC, то FG – средняя линия ∆SBC.

FG = 1/2·BC

FG= 1/2

Рассмотрим равнобедренную трапецию AFGD.

Найдем ND:

AN = AD – ND

AN = 1 – 1/4 = 3/4

Из прямоугольного треугольника ∆GND по теореме Пифагора найдем GN:

GN² = GD² – ND²

GN² = (√3/2)² – (1/4)² = 3/4 – 1/16 = 11/16

GN = √11/4

Из прямоугольного треугольника ∆AGN найдем tgα:

Угол ∠NAG = ∠AGF = ∠α, как накрест лежащие углы при AD || FG и AG – секущей.

Рассмотрим прямоугольный треугольник ∆FMG:

FM = FG·sinα

Учитывая, что угол ∠α – острый угол, найдем sinα. Воспользуемся формулой:

Тогда

Треугольники ∆AFG и ∆AKG равны, то FM = MK

Подставим полученные данные в формулу (1), получим

Ответ: 

Понравилось? Нажмите