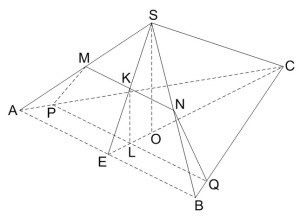
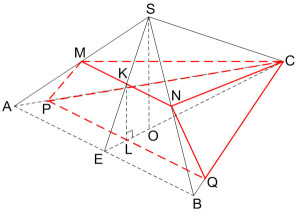
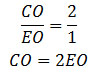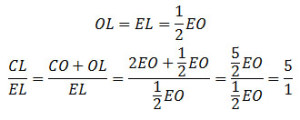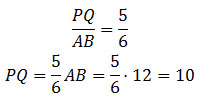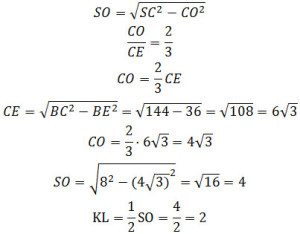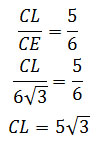Задание 14. Математика ЕГЭ. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N – середины ребер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.

Задание.

В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA  равно 8. Точки M и N – середины ребер SA и SB соответственно. Плоскость α содержит прямую MN  и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость α  делит медиану CE основания в отношении 5:1, считая от точки C.

б) Найдите объем пирамиды, вершиной которой является точка С, а основанием – сечение пирамиды SABC плоскостью α.

Решение:

а) Докажите, что плоскость α  делит медиану CE основания в отношении 5:1, считая от точки C.

Так как точки M и N – середины ребер SA и SB, то MN  – средняя линия треугольника ABS, то есть MN II AB.  AB лежит в плоскости (ABC), следовательно MN II (ABC), поэтому сечение (плоскость α) пересекает плоскость ABC по прямой PQ, параллельной MN. Таким образом, секущая плоскость представляет собой трапецию MNQP.

Так как SABC – правильная пирамида, то точка О – центр основания пирамиды, СЕ – медиана треугольника ABC. Медиана СЕ треугольника ABC делится точкой О в отношении 2:1.

Рассмотрим треугольник ABS. SЕ – медиана треугольника ABS. Точка К – точка пересечения плоскости MNQ и прямой MN, а также точка К – середина SЕ. Точка L – точка пересечения плоскости MNQ и прямой PQ.

Плоскость SCE пересекает плоскость MNQ по прямой KL. Плоскости SCE и MNQ перпендикулярны плоскости ABC. Следовательно, KL перпендикулярна плоскости основания ABC.

SO перпендикулярна плоскости основания ABC. Значит, KL II SO. Точка К – середина SЕ, тогда точка L – середина ЕО. KL – средняя линия треугольника SOE.

Итак, получим

б) Найдите объем пирамиды, вершиной которой является точка С, а основанием – сечение пирамиды SABC плоскостью α.

Объем пирамиды равен

Плоскость MNQ перпендикулярна плоскости ABC, следовательно CL перпендикулярна плоскости MNQ и является высотой пирамиды  CMNQP, т.е. CL = h.

Секущая плоскость представляет собой трапецию MNQP, которая является основанием пирамиды CMNQP, т.е. S_осн = S_MNQP.

Площадь трапеции MNQP равна

MN – средняя линия треугольника ABC.

Так как

Треугольники CPQ и ABC подобны, тогда

KL – высота трапеции MNPQ. KL – средняя линия треугольника SOE.

Из прямоугольного треугольника SOC по теореме Пифагора найдем SO.

Найдем высоту пирамиды CMNQP:

Тогда объем пирамиды:

Ответ:  

Понравилось? Нажмите