

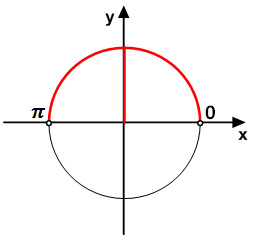
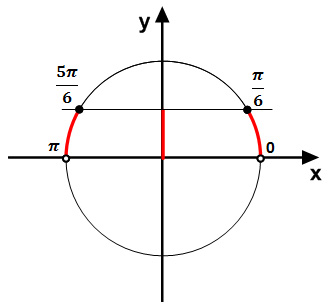
Задание 15. ЕГЭ. Решите логарифмическое неравенствоЗадание. Решите неравенство Решение: ОДЗ неравенства: sinx > 0 Преобразуем неравенство: Введем новую переменную, пусть 9t2 + 8t – 1 ≥ 0 Решим неравенство методом интервалов, найдем нули квадратного трехчлена: 9t2 + 8t – 1 = 0 D = 82 – 4·9·(-1) = 100 t1 = — 1; t2 = 1/9 t ≤ — 1 и t ≥ 1/9 Рассмотрим t ≤ — 1, вернемся к первоначальной переменной: Так как основание логарифмического неравенства 2 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: Учитывая ОДЗ, получим неравенство: Рассмотрим t ≥ 1/9, вернемся к первоначальной переменной: Так как основание логарифмического неравенства 2 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: Данное неравенство невозможно. Ответ: Оставить комментарий |
Рубрики
|
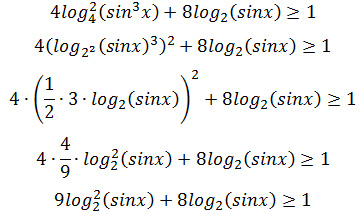
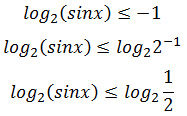
4 * 4/9 = 9 ??????????????????
4 * 9/4 надо!