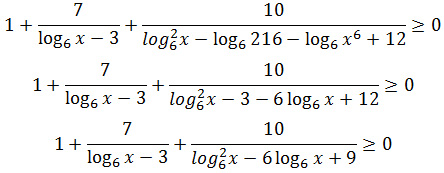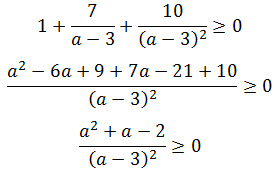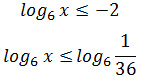Задание 15. ЕГЭ. Решите неравенство

Задание. Решите неравенство

Решение:

ОДЗ неравенства: x > 0

Преобразуем неравенство:

Введем новую переменную, пусть

Получим неравенство:

Разложим квадратный трехчлен a² – 6a + 9 на множители: a² – 6a + 9 = (a – 3)², получим

Решим неравенство методом интервалов:

Нули числителя:

a² + a – 2 = 0

D = 9

a₁ = – 2 и a₂ = 1

Нули знаменателя: 3

Получим:

a ≤ — 2;

1 ≤ a < 3;

a > 3

Рассмотрим a ≤ — 2, вернемся к первоначальной переменной:

Так как основание логарифмического неравенства 6 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: x ≤ 1/36

Рассмотрим 1 ≤ a < 3, вернемся к первоначальной переменной:

Так как основание логарифмического неравенства 6 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: 6 ≤ x < 216

Рассмотрим a > 3, вернемся к первоначальной переменной:

Так как основание логарифмического неравенства 6 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: x > 216

Найдем общее решение, учитывая ОДЗ неравенства (x > 0):

Ответ:

Понравилось? Нажмите