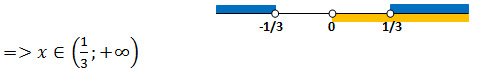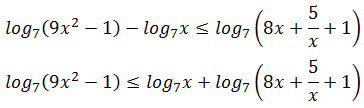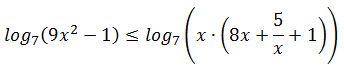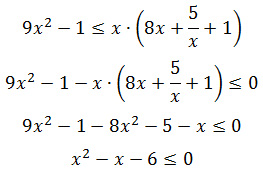Задание 15. ЕГЭ. Решите неравенство log(9x^2-1)-logx

Рубрика Задание 15, Решаем ЕГЭ по математике Комментарии (0)

Задание. Решите неравенство

Решение:

ОДЗ неравенства:

Решим первое неравенство (3x – 1)(3x + 1) > 0 методом интервалов, найдем нули квадратного трехчлена:

x₁ = — 1/3; x₂ = 1/3

x ∈ (-∞; -1/3) ∪ (1/3; +∞)

Решим третье неравенство, найдем нули числителя:

8x² + x + 5 = 0

D = 1² — 4·8·5 = — 159 <0

Нулей числителя нет, следовательно, неравенство больше нуля при x > 0.

Объединяя решения трех неравенств, получим

Преобразуем неравенство:

Сумма логарифмов равна логарифму произведения подлогарифмических выражений:

Так как основание логарифмического неравенства 7 > 1, то логарифмическое неравенство равносильно неравенству того же смысла:

Решим неравенство методом интервалов:

x² – x – 6 = 0

D = (-1)² — 4·1·(-6) = 25

x₁ = -2  и x₂ = 3

x ∈ (-2; 3)

Учитывая ОДЗ неравенства, найдем его решение:

Ответ: (1/3;3]

Понравилось? Нажмите