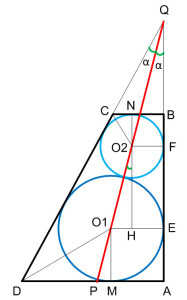
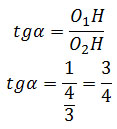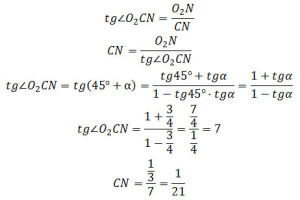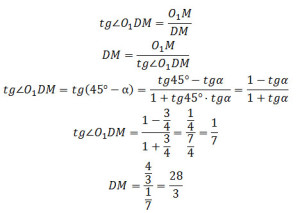Задание 16. Математика ЕГЭ. В прямоугольной трапеции ABCD с прямым углом при вершине А расположены две окружности. Найдите площадь трапеции

Задание. В прямоугольной трапеции ABCD с прямым углом при вершине А расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания ВС и первой окружности.

а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sinD.

б) Найдите площадь трапеции, если радиусы окружностей равны 4/3 и 1/3.

Решение: 

а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sinD.

 

Пусть точка Q – точка пересечения продолжений боковых сторон CD и АВ прямоугольной трапеции ABCD. Так как стороны угла ∠AQD являются касательными к окружностям, то прямая QP, проходящая через центры окружностей, является биссектрисой угла ∠AQD и треугольника ∆ AQD.

По свойству биссектрисы треугольника

 Так как треугольник ∆ AQD – прямоугольный, то

Следовательно,

б) Найдите площадь трапеции, если радиусы окружностей равны 4/3 и 1/3.

Площадь трапеции равна

(1)

Окружность с центром О₁ радиуса R = 4/3 касается боковой стороны АВ в точке Е, а основание AD касается в точке М. Тогда R = O₁E = AE = AM = O₁M = 4/3.

Окружность с центром О₂ радиуса r = 1/3 касается боковой стороны АВ в точке F, а основание BC касается в точке N. Тогда r = O₂N = NB = BF = O₂F = 1/3.

O₁H = O₁E – HE = R – r

O₁H = 4/3 – 1/3 = 1

Так как линия центров окружностей проходит через их точку касания, то

O₁O₂ = R + r

O₁O₂ = 4/3 + 1/3 = 5/3

Из прямоугольного треугольника ∆O₁O₂H по теореме Пифагора найдем О₂Н:

О₂Н² = О₁О₂² – О₁Н²

О₂Н² = (5/3)² – 1² = 16/9

О₂Н² = 4/3

О₂Н = FE = 4/3

AB = AE + FE + BF = r + FE + R

AB = 1/3 + 4/3 + 4/3 = 9/3 = 3

Угол ∠AQP = ∠HO₂O₁ = α

Из прямоугольного треугольника ∆O₁O₂H найдем тангенс угла α:

Рассмотрим прямоугольный треугольник ∆BQC, угол ∠BQC = 2α, тогда внешний угол ∠BCD треугольника ∆BQC равен:

∠BCD = ∠QBC + ∠BQC

∠BCD = 90° + 2α

Так как СО₂ – биссектриса угла ∠BCD, то ∠О₂CN половине угла ∠BCD:

Из прямоугольного треугольника ∆O₂CN найдем тангенс угла ∠O₂CN:

BC = CN + NB

BC = CN + r

BC = 1/21 + 1/3 = 8/21

Рассмотрим прямоугольный треугольник ∆ADQ, угол ∠AQD = 2α, тогда угол ∠ADQ

∠ADQ = ∠DAQ – ∠AQD

∠ADQ = 90° – 2α

Так как DО₁ – биссектриса угла ∠ADQ, то ∠О₁DM половине угла ∠ADQ:

Из прямоугольного треугольника ∆O₁DM найдем тангенс угла ∠O₁DM:

AD = DM + AM

AD = DM + R

AD = 28/3 + 4/3 = 32/3

Подставим полученные данные в формулу (1), получим:

Ответ:  

Понравилось? Нажмите