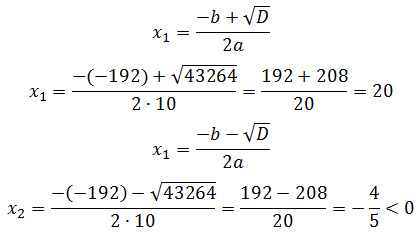Задание 11. ЕГЭ. Расстояние между пристанями А и В равно 96 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась моторная лодка

Задание. Расстояние между пристанями А и В равно 96 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 44 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

Решение:

Пока моторная лодка проделала путь из А в В и обратно, плот проплыл 44 км. Так как скорость течения реки 4 км/ч, то плот затратил на этот путь 44 : 4 = 11 ч.

Учитывая, что моторная лодка отправилась через 1 час после плота, то время в пути моторной лодки будет равно 11 – 1 = 10 ч.

Пусть x – скорость моторной лодки в неподвижной воде,

тогда скорость лодки по течению реки равна (x + 4) км/ч,

а скорость лодки против течения реки равна (x – 4) км/ч.

На путь из А в В по течению реки моторная лодка затратила 96/(x + 4) ч.,

на обратный путь против течения реки моторная лодка затратила 96/(x – 4) ч.

Время моторной лодки в пути равно 10 ч., получим уравнение:

Упростим уравнение, для этого умножим обе части уравнения на  (x + 4)·(x – 4), получим

96·(x + 4) + 96·(x – 4) = 10·(x + 4)·(x – 4)

96x + 384 + 96x – 384 – 10x² + 160 = 0

10x² – 192x – 160 = 0

D = b² – 4ac

D = (-192)² – 4·10·(-160) = 43264

Так как скорость лодки не может быть отрицательной величиной, получим ее скорость в неподвижной воде 20 км/ч.

Ответ: 20

 P.S. Для извлечения квадратного корня из числа 43264 можно воспользоваться следующим способом:

Определим, между какими числами лежит результат корня. Для этого разобьем число 43264 на группы по две цифры, начиная справа налево, у нас получилось три группы чисел 4.32.64, т. е.    необходимо подбирать числа кратные 100. Результат корня будет лежать между числами 200 и 300, так как

200² = 40000 и 300² = 90000.

Т. е.

40000 < 43264 < 90000

или

Далее определяем, как число 43264 расположено относительно чисел 40000 или 90000. Получается, что число 43264 расположено ближе к 40000, чем к 90000. Поэтому результат корня будет меньше 250.

Пробуем возводить в квадрат числа 250, 240, … Это умножение легко выполнить в столбик.

Получаем:

250² = 250·250 = 62500

240² = 240·240 = 57600

230² = 230·230 = 52900

220² = 220·220 = 48400

210² = 210·210 = 44100

200² = 200·200 = 40000

Можно сделать вывод, что

40000 < 43264 < 44100

или

Так как число 43264 оканчивается цифрой 4, то в квадрат необходимо возводить числа, расположенные между 200 и 210 и оканчивающиеся на 2 или 8, таких чисел два:

202² = 202·202 = 40804

208² = 208·208 = 43264

Следовательно,

Понравилось? Нажмите