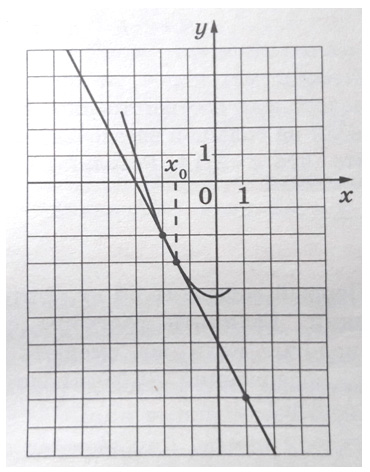
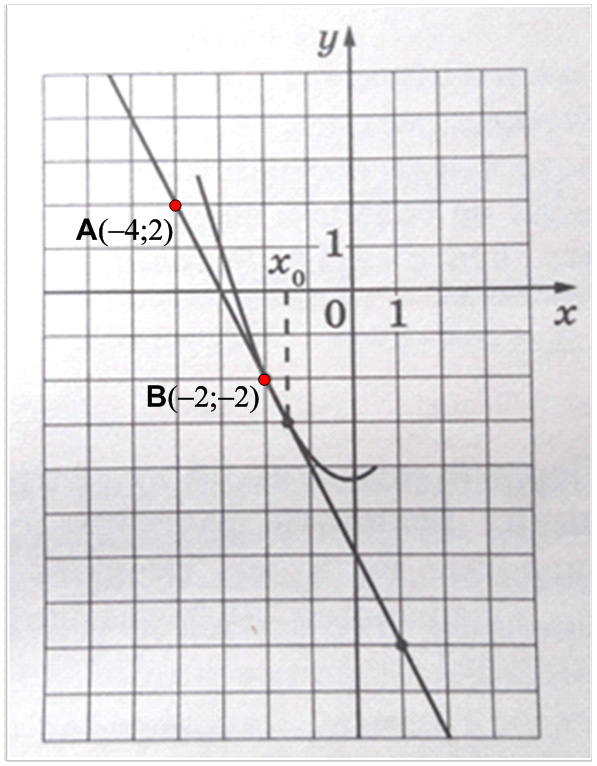
Задание 7. ЕГЭ. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0.Задание. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Решение: 1 способ: Геометрический смысл производной состоит в том, что значение производной функции f(x) в точке x0 равно угловому коэффициенту касательной к графику функции в точке x0, т. е. Число k = tga является угловым коэффициентом касательной к графику функции, а угол α — углом между касательной и осью Оx. Используя рисунок, найдем tgα. Угол α, который составляет касательная с положительным направлением оси Оx, тупой. Следовательно, значение производной функции f(x) в точке x0, отрицательно, поэтому находим тангенс смежного с ним угла β. Для этого найдем треугольник с удобными значениями катетов (см. рисунок). Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету, т. е. Тогда, тангенс тупого, смежного угла a равен: tgα = — 2. Ответ: — 2 2 способ: Значение производной функции f(x) в точке x0 равно угловому коэффициенту касательной к графику функции в точке x0, т. е. Уравнение касательной (прямой) y = kx + b, где k – угловой коэффициент касательной. На касательной выберем любые две точки с удобными координатами (см. рисунок) и найдем эти координаты. Подставим координаты точек в уравнение y = kx + b. Для точки А(-4; 2) получим: 2 = — 4k + b. Для точки В(-2; -2) получим: — 2 = — 2k + b. Имеем систему уравнений: Умножим первое уравнение системы на – 1, получим Решим систему линейных уравнений методом сложения. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной: Следовательно, значение производной функции f(x) в точке x0 равно Ответ: — 2 Оставить комментарий |
Рубрики
|