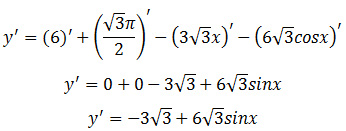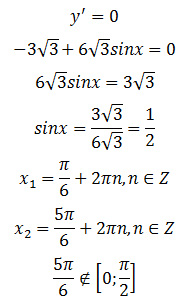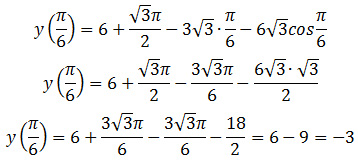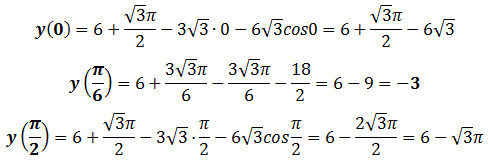Задание 12. ЕГЭ. Найдите наименьшее значение функции y = 6 + √3π/2 — 3√3x — 6√3·cosx на отрезке [0; π/2]

Задание. Найдите наименьшее значение функции

на отрезке [0; π/2].

Решение:

Найдем точку экстремума, для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.

Область определения функции: R.

Найдем производную функции:

Найдем нули производной:

Отметим точки 0, π/6 и π/2 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную:

В точке x = π/6 производная функции меняет знак с отрицательного на положительный, значит, это искомая точка минимума функции на отрезке [0; π/2].

Найдем значение функции при x = π/6:

Значение y(π/6) = — 3 является наименьшим значением функции на отрезке [0; π/2].

Ответ: — 3

P. S. Наименьшее значение функции y = 6 + √3π/2 — 3√3x — 6√3·cosx на отрезке [0; π/2] можно найти другим способом. После нахождения экстремума функции, достаточно вычислить значения функции на концах отрезка и в точке экстремума:

Ответ: -3

Понравилось? Нажмите