

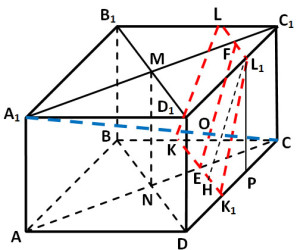
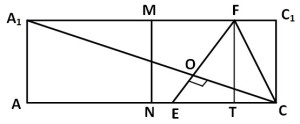
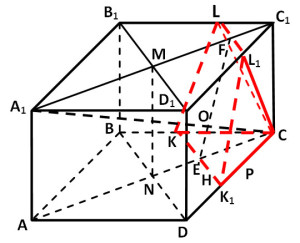
Задание 14. Математика ЕГЭ. Дана правильная четырехугольная призма ABCDA1B1C1D1, сторона AB основания которой равна 7, а боковое ребро AA1 равно √14.Задание. Дана правильная четырехугольная призма ABCDA1B1C1D1, сторона AB основания которой равна 7, а боковое ребро AA1 равно √14. На ребрах BC и C1D1 отмечены точки K и L соответственно, причем BK = 4; C1L = 1. Плоскость γ проходит через точки K и L и параллельна прямой BD. а) Докажите, что плоскость γ перпендикулярна прямой A1C. б) Найдите объем пирамиды, вершина которой является точка C, а основанием – сечение данной призмы плоскостью γ. Решение: а) Докажите, что плоскость γ перпендикулярна прямой A1C. Проведем через точки K и L прямые, параллельные BD. Эти прямые пересекают ребро DC в точке K1 и ребро D1C1 в точке L1 (см. рис. 1). Тогда равнобедренная трапеция KK1L1L является сечением призмы ABCDA1B1C1D1 плоскостью γ. Рассмотрим плоскость ACC1. Эта плоскость пересекает прямую BD в точке N, прямую KK1 в точке E и прямую LL1 в точке F. Четырехугольник ACC1A1 – прямоугольник. Рассмотрим прямоугольный треугольник CND, так как призма ABCDA1B1C1D1 – правильная, то в основании лежит квадрат, AC – диагональ грани ABCD и угол DCN равен 450. Тогда ND = DC·sin450 ND = (7·√2)/2 AC2 = AD2 + DC2 AC2 = 72 + 72 = 2·49 = 7√2 A1C1 = AC = 7√2 Треугольник NCD подобен треугольнику ECK1, получаем: EK1 : ND = K1C : DC EK1 : ((7·√2)/2) = 3 : 7 EK1 = (3√2)/2 EC : CN = CK1 : DC EC : ((7·√2)/2) = 3 : 7 EC = (3√2)/2 Треугольник MC1D1 подобен треугольнику FC1L1, получаем: FL1 : MD1 = L1C1 : D1C1 FL1 : ((7·√2)/2) = 1 : 7 FL1 = √2/2 FC1 : MC1 = L1C1 : D1C1 FC1 : ((7·√2)/2) = 1 : 7 FC1 = √2/2 Тогда HK1 = EK1 – FL1 = (3√2)/2 – √2/2 = √2 L1P = AA1 = √14; PC = L1C1 = 1 K1P = DC – (DK1 + PC) = 7 – (4 + 1) =2 Рассмотрим прямоугольный треугольник L1PK1: L1K12 = L1P2 + K1P2 L1K12 = (√14)2 + 22 = 18 L1K1 = 3√2 Рассмотрим прямоугольный треугольник L1HK1: EF = L1H L1H2 = L1K12 – HK12 L1H2 = (3√2)2 – (√2)2 = 16 L1H = 4, EF = 4. Рассмотрим рисунок 2. ET = EC – FC1 = (3√2)/2 – √2/2 = √2 Рассмотрим прямоугольный треугольник A1CC1: A1C1 = 7√2, CC1 = AA1 = √14 Рассмотрим прямоугольный треугольник FET: FT = AA1 = √14 ET = EC – FC1 = (3√2)/2 – √2/2 = √2 То есть прямые A1C и EF перпендикулярны. Прямая KK1 параллельна прямой BD, которая перпендикулярна плоскости ACC1. Значит, прямые KK1 и EF перпендикулярны прямой A1C, поэтому прямая A1C перпендикулярна плоскости γ. б) Найдите объем пирамиды, вершина которой является точка C, а основанием – сечение данной призмы плоскостью γ. Смотри рисунок 3. Объем пирамиды равен: Так как A1C перпендикулярна плоскости сечения γ, то CO — высота пирамиды. Рассмотрим треугольник EFC (рис. 2). Найдем площадь этого треугольника: EC = (3√2)/2 ET = AA1 = √14 Площадь треугольник EFC можно найти другим способом: CO = 2S/EF Площадь основания пирамиды — это площадь сечения, т.е. площадь трапеции KL1LK1. Оставить комментарий |
Рубрики
|
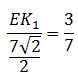
EK1 : (7·√2)/2 = 3 : 7
EK1 = (3√2)/2
Распишите, пожалуйста, как так получилось.
Смотрите уточнения.)