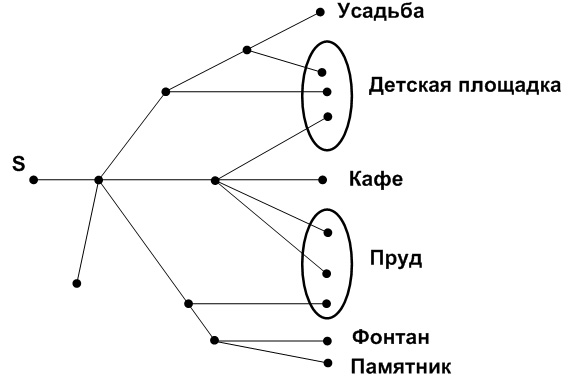
Задание 4. ЕГЭ. Артем гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно

Задание. Артем гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану.

Решение:

Рассмотрим 1 событие:

Из точки А Артем выбирает одну из четырех дрожек, тогда  вероятность выбора дорожки АВ равна 1/4.

Из точки В Артем может выбрать две из четырех дорожек к пруду, тогда вероятность попадания из точки В к пруду равна 2/4.

Тогда вероятность 1 события, т. е. того, что Артем выбирает дорожку АВ и В-Пруд, равна произведению этих вероятностей:

Рассмотрим 2 событие:

Из точки А Артем выбирает одну из четырех дрожек, тогда  вероятность выбора дорожки АС равна 1/4.

Из точки С Артем может выбрать одну из двух дорожек к пруду, тогда вероятность попадания из точки С к пруду равна 1/2.

Тогда вероятность 2 события, т. е. того, что Артем выбирает дорожку АС и С-Пруд, равна произведению этих вероятностей:

Рассмотрим 3 событие:

Из точки А Артем выбирает одну из четырех дрожек, тогда  вероятность выбора дорожки АС равна 1/4.

Из точки С Артем выбирает одну из двух дорожек к точке D, тогда вероятность выбора дорожки CD равна 1/2.

Из точки D Артем может выбрать одну из двух дорожек к фонтану, тогда вероятность попадания из точки D к фонтану равна 1/2.

Тогда вероятность 3 события, т. е. того, что Артем выбирает дорожку АС, AD и D-Фонтан, равна произведению этих вероятностей:

Все три события являются несовместными.

События называются несовместными, если в одном и том же испытании они не могут произойти одновременно, т.е наступление одного из них исключает наступление другого.

Следовательно, вероятность наступления несовместных событий, т. е. наступления или 1 события или 2 события или 3 события равна сумме вероятностей данных событий:

Р = Р₁ + Р₂ + P₃

Ответ: 0,3125

Понравилось? Нажмите