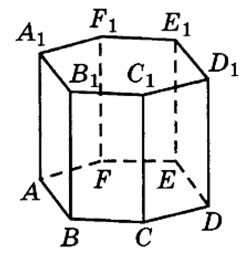
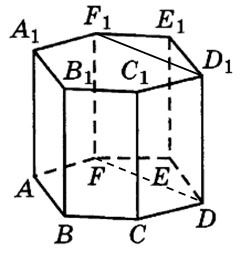
Задание 8. Математика ЕГЭ. Найти объем многогранника, вершинами которого являются вершины правильной шестиугольной призмы

Задание. Найдите объем многогранника, вершинами которого являются вершины D,  E,  F,  D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 10, а боковое ребро равно 12.

Решение:

Искомым многогранником является прямая треугольная призма с основанием FED и высотой DD1.

V = Sосн·h.

h = DD1 = 12.

Найдем площадь основания, используя для этого формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности, формулы площади треугольника.

Рассмотрим правильный шестиугольник ABCDEF, найдем сторону шестиугольника, пусть a = ED.

Найдем площадь треугольника FED:

Найдем объем искомого многогранника:

Ответ: 20.