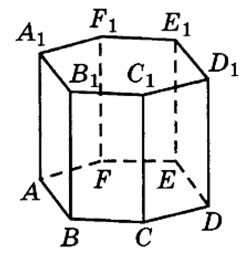
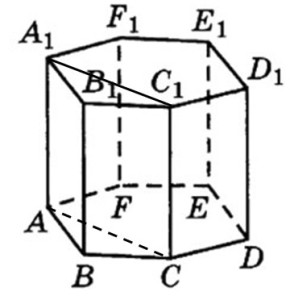
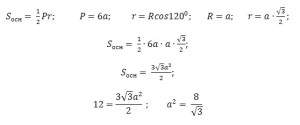Задание 8. Математика ЕГЭ. Найти объем многогранника

Задание. Найдите объем многогранника, вершинами которого являются вершины A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 5.

Решение:

Искомым многогранником является прямая треугольная призма ABCA1B1C1 с основанием ABC и высотой AA1.

V = Sосн·h.

h = AA1 = 5.

Найдем площадь основания, используя для этого формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности, формулы площади треугольника.

Рассмотрим правильный шестиугольник ABCDEF, найдем сторону шестиугольника, пусть a = AB.

Найдем площадь треугольника ABC:

Объем искомого многогранника равен: V = 2·5 = 10.

Ответ: 10.

Понравилось? Нажмите