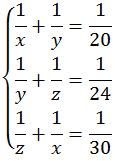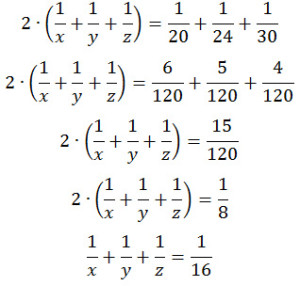Задание 22. Игорь и Паша красят забор за 20 часов.Задание. Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часов, а Володя и Игорь – за 30 часов. За сколько минут мальчики покрасят забор, работая втроем? Решение: Пусть забор – это объем работы равный 1. Игорь красит забор за x ч, тогда его производительность равна 1/x. Паша красит забор за y ч, тогда его производительность равна 1/y. Володя красит забор за z ч, тогда его производительность равна 1/z. При совместной работе производительности складываются. Игорь и Паша красят забор за 20 ч, их совместная производительность равна: Паша и Володя красят этот же забор за 24 ч, их совместная производительность равна: Володя и Игорь красят забор за 30 ч, их совместная производительность равна: Получаем систему из трех уравнений с тремя неизвестными: Решим систему методом сложения, получим Таким образом, работая вместе, Игорь, Паша и Володя красят за 1 час одну шестнадцатую часть забора, т. е. весь забор они покрасят за 16 часов или 960 минут. Ответ: 960 Оставить комментарий |
Рубрики
|