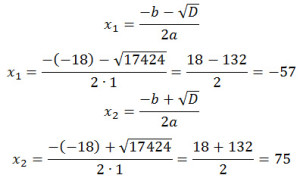Задание 22. ОГЭ. Два автомобиля одновременно отправляются в 950-километровый пробег.Задание. Два автомобиля одновременно отправляются в 950-километровый пробег. Первый едет со скоростью на 18 км/ч большей, чем второй, и прибывает к финишу на 4 ч раньше второго. Найдите скорость первого автомобиля. Решение: Пусть x км/ч – скорость первого автомобиля, а x – 18 км/ч – скорость второго автомобиля, тогда для прохождения 950 км первый автомобиль затратит а второй автомобиль затратит Так как первый автомобиль прибывает к финишу на 4 ч раньше второго, получим уравнение Учитывая, что x ≠ 0, x ≠ 18, умножим обе части уравнения на x(x – 18), получим 950·x – 950·(x – 18) = 4·x(x – 18) Раскроем скобки и приравняем к нулю: 950x – 950x + 17100 – 4x2 + 72x = 0 4x2 – 72x – 17100 = 0 x2 – 18x – 4275 = 0 D = b2 – 4ac D = (-18)2 — 4·1·(-4275) = 324 + 17100 = 17424 Первый ответ не подходит из физических соображений, поэтому скорость первого автомобиля равна 75 км/ч. Ответ: 75 P.S. Для извлечения квадратного корня из числа 17424 можно воспользоваться следующим способом: Определим, между какими числами лежит результат корня. Для этого разобьем число 17424 на группы по две цифры, начиная справа налево, у нас получилось три группы чисел 1.74.24, т. е. необходимо подбирать числа кратные 100. Результат корня будет лежать между числами 100 и 200, так как 1002 = 10000 и 2002 = 40000. Т. е. 10000 < 17424 < 40000 или Далее определяем, как число 17424 расположено относительно чисел 10000 или 40000. Получается, что число 17424 расположено ближе к 10000, чем к 40000. Поэтому результат корня будет меньше 150. Пробуем возводить в квадрат числа 150, 140, … Это умножение легко выполнить в столбик. Получаем: 1502 = 150·150 = 22500 1402 = 140·140 = 19600 1302 = 130·130 = 16900 Можно сделать вывод, что 16900 < 17424 < 19600 или Так как число 17424 оканчивается цифрой 4, то в квадрат необходимо возводить числа, расположенные между 130 и 140 и оканчивающиеся на 2, такое число одно: 1322 = 132·132 = 17424 Следовательно, Оставить комментарий |
Рубрики
|