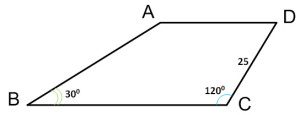
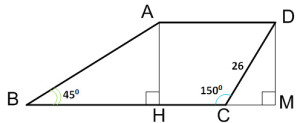
Задание 24. ОГЭ. Найдите боковую сторону АВ трапеции АВСD, если углы АВС и ВСD равны соответственно 30 и 120, а CD = 25.

Задание. 

Найдите боковую сторону АВ трапеции АВСD, если углы АВС и ВСD равны соответственно 30⁰ и 120⁰, а CD = 25.

Решение:  

В трапеции ABCD проведем высоты АН и DM.

Рассмотрим прямоугольный треугольник ∆DMC.

Угол ∠DСM и ∠ВСD – смежные углы, тогда

∠DСM + ∠ВСD = 180⁰

∠DСM = 180⁰ – ∠ВСD = 180⁰ – 120⁰ = 60⁰

DM = DC·sin∠DСM

DM = 25·sin60⁰

Рассмотрим прямоугольный треугольник ∆АВН: АН = DM,  ∠АВН = 30⁰.

АН – катет, лежащий против угла в 30⁰, следовательно, он равен половине гипотенузы, а гипотенуза АВ = 2·АН.

Получим, боковая сторона АВ = 25√3

Ответ: 25√3

Понравилось? Нажмите