

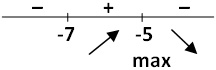
Задание 12. ЕГЭ. Найдите точку максимума функции y = (x + 7)^2 · e^( – 1 – x).Задание. Найдите точку максимума функции y = (x + 7)2 · e – 1 – x. Решение: Точка максимума функции — это точка экстремума функции, в которой производная меняет свой знак с положительного на отрицательный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю. Найдем производную заданной функции: Найдем нули производной: y′ = 0 e – 1 – x ·(x + 7)·(–x – 5) = 0 e – 1 – x > 0 (x + 7)·(–x – 5) = 0 x1 = – 7 и x2 = – 5 Отметим точки – 7 и – 5 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок) В точке х = – 5 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума. Ответ: — 5 Оставить комментарий |
Рубрики
|

А где (x+7)^2 это разве не нужно возводить в квадрат?
Можно возвести в квадрат. Но удобнее этого не делать.