

Задание 22. ОГЭ. Первый велосипедист выехал из поселка по шоссе со скоростью 24 км/ч. Через час после него со скоростью 21 км/ч из того же поселка в том же направлении выехал второй велосипедист,Задание. Первый велосипедист выехал из поселка по шоссе со скоростью 24 км/ч. Через час после него со скоростью 21 км/ч из того же поселка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого. Решение: Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догонит второго велосипедиста, тогда до места встречи со вторым велосипедистом третий пройдет x·t км. Скорость второго велосипедиста 21 км/ч, а t + 1 – время, за которое его догонит третий велосипедист (так как второй велосипедист вышел на один час раньше), тогда до места встречи с третьим велосипедистом второй пройдет 21·(t + 1) км. Так как эти расстояния одинаковые, получим 1 уравнение системы: x·t = 21·(t + 1). Скорость третьего велосипедиста x км/ч, а t + 9 ч – время, за которое он догонит первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий пройдет x·(t + 9) км. Скорость первого велосипедиста 24 км/ч, t + 11 – время, за которое его догонит третий велосипедист (так как первый вышел на 2 часа раньше третьего, а третий догнал его через 9 часов после второго), тогда до места встречи с третьим велосипедистом первый пройдет 24·(t + 11) км. Так как эти расстояния одинаковые, получим 2 уравнение системы: x·(t + 9) = 24·(t + 11) Решим получившуюся систему уравнений: Раскроем скобки в каждом из уравнений Вычтем из второго уравнение первое, получим 9x = 3t + 243 3x = t + 81 Подставим значение x в первое уравнение системы, получим t2 + 81t = 63t + 63 t2 + 18t – 63 = 0 D = b2 – 4ac D = 182 — 4·1·(-63) = 324 + 252 = 576 Первый ответ не подходит из физических соображений, поэтому Следовательно, скорость третьего велосипедиста равна 28 км/ч. Ответ: 28 P.S. Для извлечения квадратного корня из числа 576 можно воспользоваться следующим способом: Разложим число 576 на простые множители: Число 576 при разложении дает произведение множителей 576 = 2·2·2·2·2·2·3·3 Вычисляем корень из числа 576: Оставить комментарий |
Рубрики
|
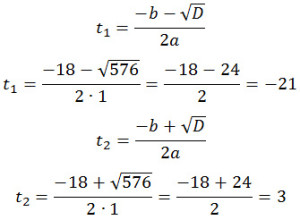
спасибо, всё ясно