

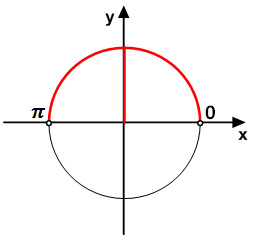
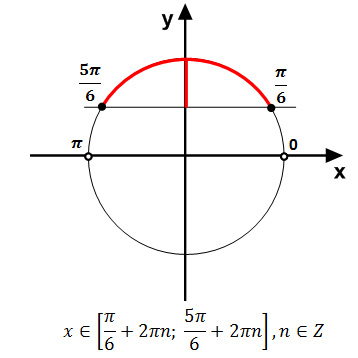
Задание 15. ЕГЭ. Решите логарифмическое неравенство 4log^2(sin^3x)+8log(sinx)<1Задание. Решите неравенство Решение: ОДЗ неравенства: sinx > 0 Преобразуем неравенство: Введем новую переменную, пусть 9t2 + 8t – 1 ≤ 0 Решим неравенство методом интервалов, найдем нули квадратного трехчлена: 9t2 + 8t – 1 = 0 D = 82 – 4·9·(-1) = 100 t1 = — 1; t2 = 1/9 — 1 ≤ t ≤ 1/9 Вернемся к первоначальной переменной: Так как основание логарифмического неравенства 2 > 1, то логарифмическое неравенство равносильно неравенству того же смысла: Получим систему неравенств: Учитывая ОДЗ, решим 1 неравенство системы: Решим 2 неравенство системы: Данное неравенство невозможно. Ответ: Оставить комментарий |
Рубрики
|
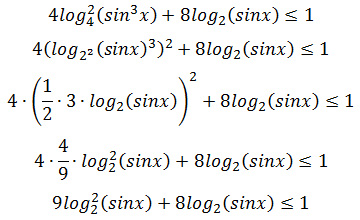


Елена Васильевна,добрый день! Вы просто умничка. Спасибо вам большое. Столько времени занимает подготовка в 11 классе к консультациям.На вашем сайте столько всего полезного, все достаточно разборчиво и доступно в пояснении.Всего вам доброго!
Спасибо!)
Каким образом (1/2) * 3 превратилось в 4/9?
Спасибо. В данном случае описка, должно быть 9/4.